Programowanie (PWr Lato 2025) Komentarze do list

Format rozwiązań

Nazwa pliku z rozwiązaniami listy x powinna być następująca {nr_indeksu}_lista_{x}.py. Struktura pliku poniższa:

# Funkcje pomocnicze do zadania 1

def zadanie_1(): ...

# Funkcje pomocnicze do zadania 2

def zadanie_2(): ...

# Funkcje pomocnicze do zadania 3

def zadanie_3(): ...

if __name__ == "__main__"":
    zadanie_1()
    zadanie_2()
    zadanie_3()

Lista 1

Komentarze i ciekawostki:

  1. Zdefiniowana funkcja “zna” swoją nazwę (i wie dużo więcej o sobie). Poniższa funkcja ma też docstring oraz zdefinowane typy wejścia i wyjścia. Zarówno anotacje, jak i magiczne metody zaczynające się od __ pojawią się dalej na wykładzie.
def minimum(lista: list[int]) -> int:
    """Szukamy minimum."""
    return min(lista)


def maksimum(lista: list[int]) -> int:
    """Szukamy maksimum."""
    return max(lista)


for funkcja in [maksimum, minimum]:
    print(funkcja.__name__)
    print(funkcja.__doc__)
    print(funkcja.__annotations__)
maksimum
Szukamy maksimum.
{'lista': list[int], 'return': <class 'int'>}
minimum
Szukamy minimum.
{'lista': list[int], 'return': <class 'int'>}
  1. W pythonie dobrą praktyką są krótkie linijki, maks 88 znaków. Łatwiej wtedy czyta się kod. Są do tego formattery, które robią to za nas. Ja polecam Ruff, dostępny jako wtyczka do VSC. Zamiast tego:
def generuj_liste_napisow_AB(dlugosc, dlugosc_napisu):
    return [''.join(random.choices(['A', 'B'], weights=[95, 5], k=dlugosc_napisu)) for _ in range(dlugosc)]

Dostajemy:

def generuj_liste_napisow_AB(dlugosc, dlugosc_napisu):
    return [
        "".join(
            random.choices(
                ["A", "B"],
                weights=[95, 5],
                k=dlugosc_napisu,
            )
        )
        for _ in range(dlugosc)
    ]
  1. Nie robimy tak:
def czy_jednomodalna(A):
    maksima = maksima_lokalne(A)
    if len(maksima) == 1:
        return True
    else:
        return False

Tylko tak:

def czy_jednomodalna(A):
    return len(maksima_lokalne(A)) == 1
  1. Biblioteka string posiada dużo pomocniczych opcji w zakresie napisów. Nie musimy wymieniać liter alfabetu, wystarczy użyć:
import string

print(string.ascii_lowercase)
abcdefghijklmnopqrstuvwxyz

Przykładowe podejście do zadania 2, inne od wykładowego. Definujemy funkcję bisekcji oraz dekorator do pomiaru czasu:

import math
from time import perf_counter_ns

import matplotlib.pyplot as plt


def measure_time(func, repeat=1):
    """Mierzy czas wykonania funkcji.

    Zwraca funkcję owiniętą w pętlę powtórzeń.
    Funkcja wynikowa zwraca listę czasów.
    """
    def worker(*args, **kwargs):
        times = []
        for _ in range(repeat):
            start_time = perf_counter_ns()
            _ = func(*args, **kwargs)
            end_time = perf_counter_ns()
            times.append(end_time - start_time)
        return sorted(times)

    return worker


def bisection(
    func, a: float, b: float, tol: float = 1e-6, max_iter: float = 1_000
) -> float:
    if func(a) * func(b) >= 0:
        return None  # Brak gwarancji istnienia miejsca zerowego

    for _ in range(max_iter):
        c = (a + b) / 2
        if abs(func(c)) < tol:
            return c
        if func(c) * func(a) < 0:
            b = c
        else:
            a = c
    return None

Mierzymy czas:

import math


def atan_minus_1(x):
    return math.atan(x) - 1


n_max = 1_000
repeat = 100
ns = list(range(1, n_max + 1))
measure_bisection_time = measure_time(bisection, repeat=repeat)
time_lists = [(n, measure_bisection_time(atan_minus_1, 0.0, 10.0 * n)) for n in ns]
time_points = [
    (float(n), time)
    for n, times in time_lists
    for time in times[repeat // 2 - 5 : repeat // 2 + 5]
]

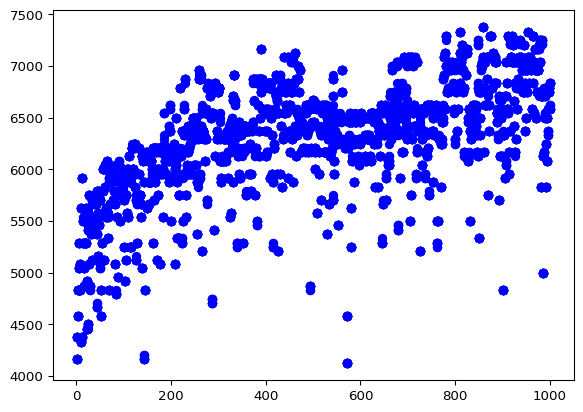
Przedstawiamy na wykresie:

import numpy as np

x, y = zip(*time_points)
fig, ax = plt.subplots()
ax.plot(x, y, "o", color="blue")

Lista 2

  1. W opowiastce o Alfredzie, wczytując się dokładnie, mógł on się także cofać, co oznacza przyzwolenie na ujemne rozwiązania. Przyjmowałem też rozwiązania zakładające jedynie dodatnią ilośc skoków.

  2. Nie robimy tak:

def moja_funkcja(k):
    return k


nazwa = "moja_funkcja"
wynik = eval(nazwa)(1)
print(f"Funkcja {nazwa} daje {wynik=}")
Funkcja moja_funkcja daje wynik=1

Funkcja eval ma bardzo mało rozsądnych zastosowań, jest niebezpieczna, najlepiej zapomniec że istnieje. Zamiast tego:

funkcja = moja_funkcja
wynik = moja_funkcja(1)
print(f"Funkcja {funkcja.__name__} daje {wynik=}")
Funkcja moja_funkcja daje wynik=1
  1. Staramy się o czyste i jasne importy z modułów. Możemy robić tak:
from math import ceil, gcd, lcm

print(lcm(gcd(10, 6), ceil(10 / 3)))
4

(kolejność funkcji alfabetyczna) lub tak

import math

print(math.lcm(math.gcd(10, 6), math.ceil(10 / 3)))

Staramy się nie robić tak:

from math import lcm, ceil
import math

print(lcm(math.gcd(10, 6), ceil(10 / 3)))

Nigdy nie robimy tak:

from math import *

Lista 3

  1. W funkcji liczby_zaprzyjażnione można użyć cachowania aby dla każdej liczby liczyć jej sumę dzielników tylko raz.
def liczby_zaprzyjaźnione(N):
    liczby = []
    sumy_dzielników = [0] * (N + 1)
    for a in range(2, N):
        b = suma_dzielników(a)
        sumy_dzielników[a] = b
        if b < a:
            if sumy_dzielników[b] == a:
                liczby.append((a, b))
    return liczby
  1. Iterując po obiekcie, chcąc znać indeks na ktorym jesteśmy używamy enumerate.
lista = ["a", "b"]

# nie robimy tak
licznik = 0
for litera in lista:
    print(f"{licznik}: {litera}")
    licznik += 1

# tylko tak
for licznik, litera in enumerate(lista):
    print(f"{licznik}: {litera}")
0: a
1: b
0: a
1: b
  1. Sito Eratostenesa da się znacząco przyśpieszyć implementując je w NumPy.
import numpy as np
import time


def sito_listowe(limit):
    """Implementacja sita Eratostenesa przy użyciu list."""
    if limit < 2:
        return []
    kandydaci = list(range(limit))
    kandydaci[0] = None
    kandydaci[1] = None
    for liczba in kandydaci:
        if liczba is None:
            continue
        if liczba * liczba >= limit:
            break
        for wielokrotnosc in range(liczba * liczba, limit, liczba):
            kandydaci[wielokrotnosc] = None
    return [liczba for liczba in kandydaci if liczba is not None]


def sito_numpy(limit):
    """Implementacja sita Eratostenesa przy użyciu biblioteki NumPy."""
    if limit < 2:
        return np.array([], dtype=int)

    czy_pierwsza = np.ones(limit + 1, dtype=bool)
    czy_pierwsza[0:2] = False
    for p in range(2, int(np.sqrt(limit)) + 1):
        if czy_pierwsza[p]:
            czy_pierwsza[p * p :: p] = False
    return np.nonzero(czy_pierwsza)[0]


def mierz_czas_sita(funkcja, limit, nazwa_funkcji, powtorzenia=10):
    """Mierzy czas wykonania danej funkcji sita Eratostenesa."""
    czasy = []
    for _ in range(powtorzenia):
        czas_start = time.time()
        wynik = funkcja(limit)
        czas_koniec = time.time()
        czasy.append(czas_koniec - czas_start)

    minimalny_czas = min(czasy)
    print(f"{nazwa_funkcji} (limit={limit}):")
    print(f"  Minimalny czas ({powtorzenia} uruchomień): {minimalny_czas:.6f} sekund")
    print(f"  Liczba liczb pierwszych: {len(wynik)}")


# Przykładowe użycie i pomiar czasu
limit = 1_000_000

print("Pomiar czasu z limitem =", limit)
mierz_czas_sita(sito_numpy, limit, "Sito NumPy (zoptymalizowane)")
mierz_czas_sita(sito_listowe, limit, "Sito Listowe")
Pomiar czasu z limitem = 1000000
Sito NumPy (zoptymalizowane) (limit=1000000):
  Minimalny czas (10 uruchomień): 0.001593 sekund
  Liczba liczb pierwszych: 78498
Sito Listowe (limit=1000000):
  Minimalny czas (10 uruchomień): 0.081699 sekund
  Liczba liczb pierwszych: 78498

Lista 4

  1. Często pojawia się policzenia powtórzeń elementów w liśicie:
lista = [1, 2, 2, 1, 2, 3, 4, 2, 1, 3]
wystapienia = {klucz: 0 for klucz in set(lista)}
for elem in lista:
    wystapienia[elem] += 1
print(wystapienia)
{1: 3, 2: 4, 3: 2, 4: 1}

Python ma do tego wbudowaną funkcjonalność Counter:

from collections import Counter
wystapienia = Counter(lista)
print(wystapienia)
Counter({2: 4, 1: 3, 3: 2, 4: 1})
  1. Podobnie mamy gotowe narzędzia do liczenia sum częściowych. Zamiast:
pozycje = {}
suma = 0
klucze = sorted(wystapienia)
for klucz in klucze:
    pozycje[klucz] = suma
    suma += wystapienia[klucz]
print(pozycje)
{1: 0, 2: 3, 3: 7, 4: 9}

możemy użyć accumulate:

from itertools import accumulate


pozycje = dict(
    zip(
        klucze,
        accumulate((wystapienia[k] for k in klucze), initial=0),
    )
)
print(pozycje)
{1: 0, 2: 3, 3: 7, 4: 9}
  1. Alternatywne podejście do sortowania przez zliczanie. Dobry pretekst aby poznać defaultdict oraz chain.
from collections import defaultdict
from itertools import chain


def sortowanie_zliczanie(lista, klucze):
    wystapienia = defaultdict(list)
    for elem in lista:
        wystapienia[elem].append(elem)
    return list(
        chain.from_iterable(
            (wystapienia[klucz] for klucz in klucze),
        )
    )


print(
    sortowanie_zliczanie(
        ["a", "c", "a", "b", "b"],
        klucze=("c", "b", "a"),
    )
)
['c', 'b', 'b', 'a', 'a']
Back to top