Strategies for Numerical Integration

Numerical integration

Calculation of many financial methods or metrics relies on a mathematical tool called numerical integration. In simple terms, numerical integration takes a function that represents a continuous process (like the changing value of an investment over time) and approximates the area under its curve. This area can then be used to calculate important quantities, like the total return of the investment or price of a derivative instrument.

So we are tasked with a problem, and one that has many different ways of solving, or rather approximating the solution. You most likely (taking into account you’re still reading this) encountered rectangle rule, or Riemann summation in your Calculus 101 course/self-learning. But there are many other techniques, which we call schemes.

For quantitative analysts, the choice of the integration method matters. Different integration schemes offer varying levels of accuracy and efficiency. Unfortunately there’s no best technique. Same algorithm can be a perfect fit for problems with certain characteristics, but unusable for others. And then there is the old as time performance vs. accuracy trade-off.

As programmers working in finance, we need to be adaptable and leverage solutions that allow us to switch between these methods seamlessly.

Design patterns

This is where design patterns come in. Design patterns are reusable solutions to common programming problems. Their widespread adoption in software development is largely attributed to the publication of Design Patterns: Elements of Reusable Object-Oriented Software in 1994. Authored by E. Gamma, R. Helm, R. Johnson, and J. Vlissides (often referred to as the “Gang of Four” or GoF), this book cataloged 23 essential software design patterns. These patterns provided solutions to common design problems in object-oriented programming, promoting code reusability, maintainability, and flexibility.

Some design patterns can feel clunky or inelegant when implemented in Python. The language itself often has built-in features or idioms that achieve the same result in a more Pythonic way (meaning it follows Python’s style and conventions). Sometimes, design patterns can be seen as overcomplicating simple problems. On the other hand, usage of well-known and understood patterns may enhance your engineering skills and improve code readability.

Ultimately, the decision of whether or not to use design patterns in Python depends on the specific context of your project and your coding style. There’s no right or wrong answer. But first, you need to know the classics to diss the classics. We’ll hold on with the dissing for now, cause in the example below chosen design pattern makes for a very clean implementation. You’ll see for yourself.

Strategy pattern

We know the stage now — one problem statement, multiple strategies to tackle. Important observation here is that we don’t actually care which one is used. When you substitute the integral value to client code — a formula or further algorithm — it’s irrelevant how it was computed, as long its correct to required level of accuracy. This means that the problem should be decoupled from algorithms to solve it. We should target a implementation where you can state a problem Calculate the integral of \(\sin(x)\) from \(0\) to \(\pi\) and then just throw different algorithms at it to obtain a solution. So let’s get coding!

Note

I will show you this pattern through an example. If you prefer more generic setup see Refactoring Guru’s implementation. The customary ‘software engineering’ example used to present the SDP is sorting a list of integers using different sorting algorithms.

Abstract schema

Each scheme that we’d come up with, even the most complex ones, would have the same main purpose — ‘integrate’. To make the implementation for it, we create a template class that all concrete schemes will inherit from.

from abc import ABC, abstractmethod
from typing import Callable

class IntegrationScheme(ABC):
    """Abstract base class for integration schemas."""

    @abstractmethod
    def integrate(
        self,
        integrand: Callable[[float], float],
        *,
        start: float,
        end: float,
    ) -> float:
        """Abstract method for integrating a function."""

Unpacking this, we already used some nifty Pythonic tricks in those few lines:

• ABC is a way of defining abstract classes. If you try to create an object of a class inheriting from ABC you’d get an error. It is used as a base class for concrete subclasses and serves as a template. Think of an example of animal and cat from the real world. You’ve never seen an abstract animal being in your life (that would be a truly transcendental experience). But you’ve hopefully seen many cats.
• Decorator @abstractmethod signifies that the method is just a mock-up. It needs to be present and overridden in all concrete classes that inherit from IntegrationScheme
• Type annotations like start: float don’t affect the script behavior in any way. Those are only for us to not get lost in Python’s dynamic typing magic. They can also be leveraged by static type checkers like mypy to flag problems with your code before you run it — just like in compiled languages.
• Callable annotation signifies a function-like object something you can call through (), like some_func(one, second=two)’ — here some_func is a callable. Calls to an object can be implemented by writing the __call__ method for the class.

Concrete schema implementations

Rectangle Rule

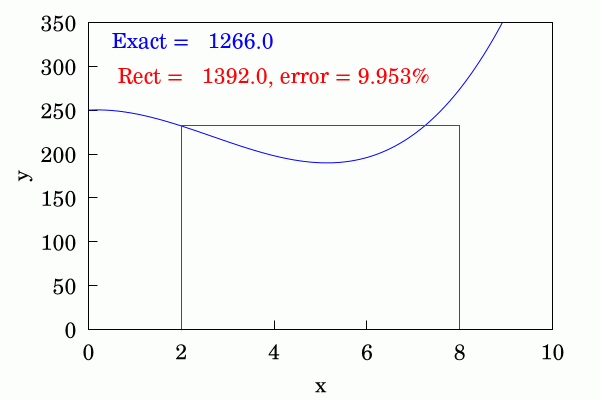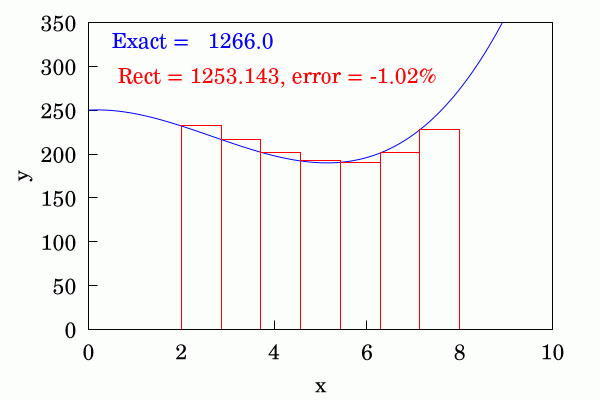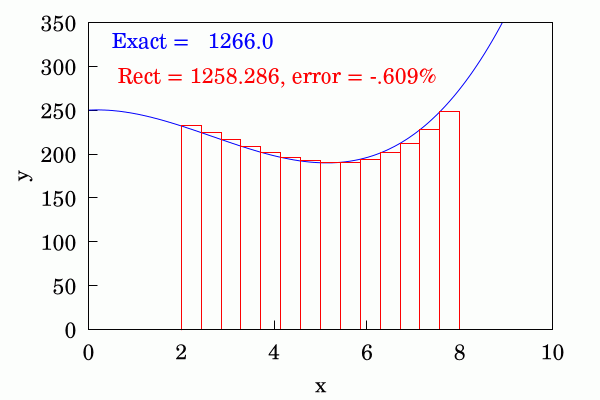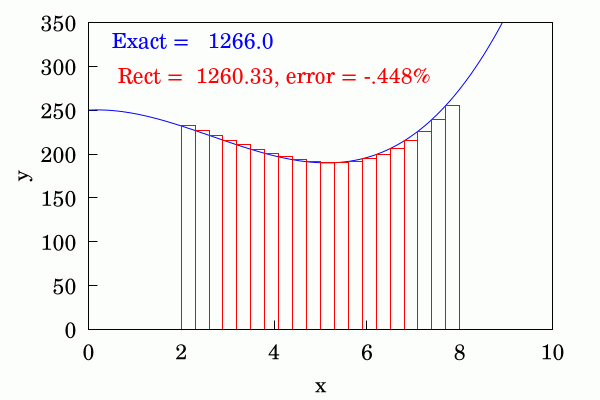
It’s the simplest way of estimating the area under a curve you can think of — cover it with smaller and smaller rectangles with the value of a function at the leftmost point as height constant width.

Implementing this idea is trivial when using numpy, but let’s add some syntactic sugar so the class is sweeter to work with.

import numpy as np

class RectangleScheme(IntegrationScheme):
    """Schema for rectangle integration."""

    def __init__(
        self,
        steps: int,
    ) -> None:
        """Initializes the rectangle integration config."""
        if steps <= 0:
            raise ValueError("Steps must be greater than 0.")
        self._steps = steps

    def __str__(self) -> str:
        """Returns the string representation of the schema."""
        return f"Rectangle schema with {self._steps} steps"

    def integrate(
        self,
        integrand: Callable[[float], float],
        *,
        start: float,
        end: float,
    ) -> float:
        """Integrates a function using rectangle integration."""
        x_points = np.linspace(start, end, self._steps)
        values = integrand(x_points)
        dx = (end - start) / np.float64(self._steps)
        return np.sum(values) * dx

• RectangleScheme subclasses IntegrationScheme so we need to implement the integrate method.
• __init__ method is run each time object of this class is requested. It sets the stage — in this case all we need is the number of rectangles we are to use. To be cautious, we check if the steps number is positive.
• __str__ is called when we try to represent the object as string — ex. in f-strings or directly calling str(). We just taught our class objects to introduce themselves nicely.
• integrate is as simple as the idea behind it:
  • get the equaly spaced x values,
  • calculate integrand values at the points,
  • sum it up,
  • multiply the sum by the distance between two consecutive points.

Simple Monte Carlo

This guy sounds fancy with its luxurious Monaco vibes, but it’s just a peasant in a nice suit. Instead of looking at equaly-spaced points, we shuffle them from uniform distribution on the interval of integration. We calculate the integrand function values at those points and sum them up. Then multiply the sum by the average distance between points and through the magic of probability theory (and not opening actual probability textbook in 10 years) you get a good probabilistic estimator of the integral value. The implementation is analogous to the RectangleScheme.

from typing import Optional

class MonteCarloScheme(IntegrationScheme):
    """Schema for Monte Carlo integration."""

    def __init__(
        self,
        random_points: int,
        random_seed: Optional[int] = None,
    ) -> None:
        """Initializes the rectangle integration config."""
        if random_points <= 0:
            raise ValueError("Points must be greater than 0.")
        self.__random_points = random_points
        self.__random_seed = random_seed

    def __str__(self) -> str:
        """Returns the string representation of the schema."""
        points_msg = f"Monte Carlo schema with {self.__random_points} random points"
        seed_msg = f" and seed {self.__random_seed}" if self.__random_seed else ""
        return f"{points_msg}{seed_msg}"

    def integrate(
        self,
        integrand: Callable[[float], float],
        *,
        start: float,
        end: float,
    ) -> float:
        """Integrates a function using Monte Carlo integration."""
        np.random.seed(seed=self.__random_seed)
        x_points = np.random.uniform(start, end, self.__random_points)
        values = integrand(x_points)
        average_dx = (end - start) / np.float64(self.__random_points)
        return np.sum(values) * average_dx

• Optional[int] annotation means that the value of random_seed can be a float or None. With a set seed we get a reproducable results — good for testing but not for actual usage. Hence the default value here is None.

Note

The Optional stands for could be None as well, it doesn’t affect if the input is mandatory or not. In our case it’s not, but thats stated by the = None part. In Python 3.11 onwards it’s recommended to use int | None instead.

Integrator

What’s left is to have a way of defining the problem to solve and define how our schemes (strategies) interact with it.

"""An integrator class that allows to perform integration using different schemas."""
from typing import Callable

class Integrator:
    """An integrator class that allows to perform integration using different
    schemas as strategies."""

    def __init__(
        self,
        integrand: Callable[[float], float],
        interval_start: float,
        interval_end: float,
    ) -> None:
        """Initializes the integrator class."""
        if interval_start >= interval_end:
            raise ValueError("Start value must be less than end value.")
        self.__integrand = integrand
        self.__interval_start = interval_start
        self.__interval_end = interval_end

    def __call__(
        self,
        schema: IntegrationScheme,
    ) -> float:
        """
        Calculates the definite integral value of a function.

        Args:
            schema: integration schema
        """
        print(f"Using {schema}.")
        return schema.integrate(
            self.__integrand,
            start=self.__interval_start,
            end=self.__interval_end,
        )

• The __init__ takes in the obvious parameters — function to integrate, start and end of the interval. It also checks if it’s a proper integral.
• We get to implement our own __call__ method now. It’s clear what Integrator class does. No need to have a method with a descriptive name like Integrator.integrate. To use it you pass through the integration scheme into the integrator — notice annotation of the abstract IntegrationScheme. It prints the info on strategy used (using the __str__ methods) and calls integrate method of the scheme. No care in the world on how the value is actually calculated.

Let’s integrate!

Ok, now to the integrating! Let’s set up the stage:

start, end = 0, np.pi / 2.0

def f(x: float) -> float:
    return np.sin(x) + np.cos(x)

Excited? Don’t be… yet.

We should get some benchmark value first. As none of us would bother to integrate this by hand, we’ll use SciPy. Unexpectedly (SciPy uses C and Fortran underneath), we get the result in a breeze and it is very close to actual value of 2.0.

from scipy.integrate import quad

scipy_quad, err = quad(f, start, end)
print(scipy_quad)

1.9999999999999998

Now let’s use our Integrator class and see.

integrator = Integrator(
    f,
    interval_start=start,
    interval_end=end,
)

iterations = [2**i for i in range(0,21,5)]
rectangle_results = [integrator(RectangleScheme(steps=i)) for i in iterations]
mc_results = [integrator(MonteCarloScheme(random_points=i)) for i in iterations]

print(f"Rectangle schema results:\n{rectangle_results}.")
print(f"Monte Carlo schema results:\n{mc_results}.")

Using Rectangle schema with 1 steps.
Using Rectangle schema with 32 steps.
Using Rectangle schema with 1024 steps.
Using Rectangle schema with 32768 steps.
Using Rectangle schema with 1048576 steps.
Using Monte Carlo schema with 1 random points.
Using Monte Carlo schema with 32 random points.
Using Monte Carlo schema with 1024 random points.
Using Monte Carlo schema with 32768 random points.
Using Monte Carlo schema with 1048576 random points.
Rectangle schema results:
[np.float64(1.5707963267948966), np.float64(1.986172817555692), np.float64(1.9995804632216618), np.float64(1.9999869013603688), np.float64(1.9999995906791057)].
Monte Carlo schema results:
[np.float64(2.1319255971531157), np.float64(2.014877742794417), np.float64(1.9897753653556745), np.float64(2.000777757422879), np.float64(2.000285046770072)].

The performance and convergence of those schemes is terrible. Like anything in Python, if you want robust and performing code, you need to implement it with C or use any/all of the enhancement frameworks that Python provides (see Numba). Additionally, the simple methods we implemented are very naive. The standard numerical packages use sophisticated algorithms honed for many decades.

But I was wrong! You should be excited! We just learned new approach for setting up extensible and readable code! Look how cleanly the problem statement is separated form different strategies to solve it.

If you are now wondering how much we could improve by using more advanced techniques (like stratified Monte Carlo or adaptive quadrature) you just need to implement new subclass of `IntegrationSchema’ and you’re done. No changes to the existing code are needed, just simple extension. And that’s the idea behind strategy pattern.

Note

Download the whole code here.